Business Statistics With Python Assignment Answer

Business Statistics With Python

Trust Native Assignment Help for all your academic needs. As a leading provider of assignment assistance in the UK, we take pride in delivering exceptional results that exceed expectations. Experience the difference with Native Assignment Help today.

Part A: Business Statistics

Question 1.

a) The value of the following probability from the question is “P (A and B) =0.”

b) The value of the following probability from the question is “P (A and C) =0.”

c) The value of the following probability from the question is “P (B and C) = P (B) x P(C) = 0.2 x 0.3 = 0.06.”

d) The value of the following probability from the question is “P (A or B) = P (A) + P (B) = 0.1 + 0.2 = 0.3.”

e) The value of the following probability from the question is “P (A or C) = P (A) + P(C) = 0.1 + 0.3 = 0.4”

f) The value of the following probability from the question is “P (B or C) = P (B) + P(C) - P (B and C) = 0.2 + 0.3 - 0.06 = 0.44.”

g) The value of the following probability from the question is “P (A and (B or C)) = P (A and B) + P (A and C) = 0 + 0 = 0

P (B and C) = P (B) * P(C) = 0.2 * 0.3 = 0.06

P (B or C) = P (B) + P(C) - P (B and C) = 0.2 + 0.3 - 0.06 = 0.44”

Finally, it can compute P (A | B or C) using the formula for conditional probability which is “P (A | B or C) = P (A and (B or C)) / P (B or C) = 0 / 0.44 = 0.”

1. h) “P (B and C | B or C) = P (B and C)/ (P (B or C))

P (B or C) = P (B) + P(C) - P (B and C)

P (B and C) = P (B) * P(C) = 0.2 * 0.3 = 0.06

P (B or C) = 0.2 + 0.3 - 0.06 = 0.44

P (B and C | B or C) = 0.06 / 0.44 ≈ 0.1364.”

Question 2.

The likelihood of a student failing this test, which is being taken in class by 28 pupils, is 5%. A student passing the test is a success, and a student failing the test is a failure. Thus, the likelihood of success is 1 - 0.05 = 0.95, while the probability of failure is 0.05 (Holman and Hasher, 2022).

The number of trials (n) and the likelihood that each trial would succeed (p) are the two parameters that comprise the binomial distribution. In this instance, p = 0.95 and n = 28. So “The Discrete Probability Distribution: x = {pass, fail} P(x) = {0.95, 0.05}.”

Let X represent the random variable that represents the proportion of the 28 students that fail the test. The likelihood of any one student failing the test is 0.05, as well as the probability of any one student passing the test, is 0.95 because each student's outcome is independent. As a result X ~ Binomial (n=28, p=0.05). To determine the likelihood that two students would fail the test exactly:

“P(X=2) = (28 choose 2) * 0.05^2 * 0.95^26

= (28! / (2! * 26!)) * 0.05^2 * 0.95^26

= 0.2692.”

As a result, the likelihood that two students would fail the test exactly is 0.2692, or roughly 26.92%.

Here to determine this probability the binomial distribution formula can be used.

“P(X ≤ 2) = P(X = 0) + P(X = 1) + P(X = 2).”

Where X is a random variable that represents how many pupils fail the test.

Where k is the number of failures, n is the total number of students, and p is the chance of failing (0.05). One can determine each of the individual probabilities using this formula.

“P(X = 0) = (28 choose 0) * 0.05^0 * 0.95^28 = 0.376

P(X = 1) = (28 choose 1) * 0.05^1 * 0.95^27 = 0.367

P(X = 2) = (28 choose 2) * 0.05^2 * 0.95^26 = 0.172”

Afterwards, one can sum them to determine the overall likelihood (Suharto, 2021).

“P(X ≤ 2) = 0.376 + 0.367 + 0.172 = 0.915”

As a result, the likelihood that fewer than two students would fail the exam is around 0.915, or 91.5%.

One must first calculate the likelihood that two or fewer students would fail the test before one can calculate the likelihood that more than two students would fail the test.

Let X represent the proportion of pupils that fail the exam. Here it can describe X as a “binomial random variable” using parameters n = 28 (the number of trials) as well as p = 0.05 because each student's success or failure is independent of the others (the probability of failure).

The “cumulative distribution function (CDF)” of the binomial distribution is then used to calculate the likelihood that two or fewer students would fail the test (Jiang, 2021).

“P(X ≤ 2) = ΣP(X = k), k = 0, 1, 2”

One can determine each term in the summation using the binomial probability formula:

“P(X = 0) = (28 choose 0) * 0.05^0 * 0.95^28 ≈ 0.34

P(X = 1) = (28 choose 1) * 0.05^1 * 0.95^27 ≈ 0.40

P(X = 2) = (28 choose 2) * 0.05^2 * 0.95^26 ≈ 0.19

Therefore, P(X ≤ 2) = 0.34 + 0.40 + 0.19 ≈ 0.93.”

The complement of this probability is the likelihood that more than two pupils would fail the test:

“P(X > 2) = 1 - P(X ≤ 2) ≈ 1 - 0.93 = 0.07.”

Hence, there is a 0.07 or 7% per cent chance that more than two pupils would fail the test.

Question 3.

The number of serious leaks can be represented as a random variable, X, with possible values ranging from 0 to 4. One can employ a discrete probability distribution to represent the likelihood of each occurrence because there are a finite number of possible outcomes.

Let p represent the likelihood that a significant leak would develop in any particular area of the water conduct. The likelihood of a portion of the water conduct having no severe leaks is (1-p), while the probability of a section having four severe leaks is p^4 (Sial et al. 2021).

The table below illustrates the probability distribution for the number of serious leaks.

X	0	1	2	3	4
“P(X)”	“(1-p)^4”	“4p(1-p)^3”	“6p^2(1-p)^2”	“4p^3(1-p)”	“p^4”

Table 1: Probability Distribution Table

Because one of the probable outcomes (0, 1, 2, 3, or 4 major leaks) must occur, the probability in the table sum up to 1.

To respond to this query, it is necessary to assume that the likelihood of discovering a significant leak remains constant over the entire water route while an inspection of the previous 3800 metres has no bearing on the likelihood of discovering leaks in the subsequent 1000 metres.

Let's use X to represent the number of serious leaks discovered in the following 1000 metres. The estimated number of serious leaks in 1000 metres of the water conduct can be modelled as a Poisson random variable with parameter.

Since one is unsure of its value of it, one must make an educated guess using the information one does have. To estimate, one can consider the number of leaks discovered over the previous 3800 metres. The number of serious leaks discovered per metre is “r = 4 / 3800 = 0.00105.”

Hence, the anticipated quantity of serious leaks per 1000 metres is “λ = r * 1000 = 1.05.”

Now, one can employ the Poisson distribution to determine the likelihood of discovering fewer than two serious leaks within the next 1000 metres (Lasser et al. 2021).

“P(X ≤ 2) = P(X = 0) + P(X = 1) + P(X = 2)

= e^ (-λ) * (λ^0 / 0!) + E^ (-λ) * (λ^1 / 1!) + E^ (-λ) * (λ^2 / 2!)

= e^ (-1.05) * (1.05^0 / 0!) + E^ (-1.05) * (1.05^1 / 1!) + E^ (-1.05) * (1.05^2 / 2!)

= 0.348.”

Thus, the likelihood that there would be fewer than two serious leaks discovered in the following 1000 metres is approximately 0.348, or 34.8%.

One can use a Poisson distribution to simulate the number of leaks in a given length of the conduct if it can be assumed that the leaks are randomly distributed throughout the conduct and that the likelihood of finding a serious leak is the same throughout the conduct.

Let be the anticipated quantity of serious leaks per conduct metre. Using the information one has, one can estimate “λ = (number of severe leaks) / (total length of conduct in meters) = 4 / 3800 = 0.0010526.”

With this value, one can use the Poisson distribution to determine the likelihood of discovering precisely two serious leaks within the next 1000 metres of the conduct: “P(X = 2) = (e^ (-λ) * λ^2) / 2! = (e^ (-0.0010526) * 0.0010526^2) / 2! = 0.000553.”

Hence, there is a roughly 0.000553 chance of discovering precisely two serious leaks in the following 1000 metres of the water channel (Xu and Freedenberg, 2021).

One must make certain assumptions regarding the distribution of leaks throughout the water conduit to respond to this query. The likelihood of discovering a serious leak in a certain metre of the water conduit, presuming that leaks are dispersed uniformly along the conduit, is given by: “p = 4/3800”. This is because one is aware that there are 4 significant leaks in the conduit's 3800 metres.

Let X represent the number of significant leaks discovered in the conduit's following 1000 metres. The likelihood that X is greater than 2 is what one is looking for. One could calculate the chance of X significant leaks in 1000 metres of the conduit using the Poisson distribution as follows: “P(X = k) = (e^ (-λ) * λ^k) / k!”

Where λ is the predicted number of leaks per 1000 metres and is calculated as follows:

“λ = (1000/3800) * 4 = 1.05.”

“P(X > 2) = 1 - P(X <= 2)

= 1 - (P(X = 0) + P(X = 1) + P(X = 2))

= 1 - [(e^ (-1.05) * 1.05^0) / 0! + (e^ (-1.05) * 1.05^1) / 1! + (e^ (-1.05) * 1.05^2) / 2!]

= 0.3405.”

Thus, there is a 0.3405 or 34.05% chance of discovering more than two serious leaks in the conduit's following 1000 metres.

Question 4.

Researchers must determine the likelihood that a screw's diameter is outside the range of 1.46 mm to 1.56 mm to calculate the probability that it is unsuitable for production.

By taking the mean away and dividing by the standard deviation, researchers can standardise the distribution of the screw's diameter: “z = (X - μ) / σ”

“z = (X - 1.50) / 0.01”

“P(X < 1.46 or X > 1.56) = P (z < (1.46 - 1.50) / 0.01 or z > (1.56 - 1.50) / 0.01)

P (z < (1.46 - 1.50) / 0.01) = P (z < -4)

P (z > (1.56 - 1.50) / 0.01) = P (z > 6)”

Hence, the likelihood that a screw cannot be produced is equal to the product of the two probabilities:

“P(X < 1.46 or X > 1.56) = P (z < -4) + P (z > 6) = 0.00003 + 0 = 0.00003.”

So, the chance that a screw won't be used in manufacturing is extremely minimal (about 0.003%).

The variable X, which is normally distributed with a mean of 1.50 mm and a standard deviation of 0.01 mm, needs to be standardised to a normal distribution with a mean of 0 and standard deviation of 1 to calculate the probability that an acceptable screw has a diameter that is less than or equal to 1.52 mm.

Suppose Z is the standardised variable.

“Z = (X - μ) / σ

Z = (1.52 - 1.50) / 0.01 = 2”

One must now calculate the likelihood that a screw would have a diameter smaller than or equal to 1.52 mm, which can be written as

“P(X ≤ 1.52 | 1.46 ≤ X ≤ 1.56)” in which P stands for probability (Berti et al. 2019).

The probability that a standardised normal variable is less than or equal to 2, which is about 0.9772, can be calculated using the standard normal distribution table.

Consequently, there is a roughly 0.9772 per cent chance that an acceptable screw would have a diameter that is less than or equal to 1.52 mm.

To resolve this issue, one must determine the likelihood that a screw with a diameter bigger than 1.50 mm satisfies the requirements for acceptable quality. To do this, one divides the total area under the curve between 1.46 mm and 1.56 mm by the area under the normal curve of distribution between 1.50 mm as well as 1.56 mm.

Let X be a random parameter corresponding to the diameter of a screw, with a mean of 1.50 mm and a standard deviation of 0.01 mm, and that is normally distributed. Then, it could be typed: “X ~ N (μ, σ)”

Where a normal distribution with a mean and a standard deviation is denoted by N (μ, σ).

“P (1.50 < X ≤ 1.56)

P(X ≤ 1.56) - P(X ≤ 1.50)”

One must normalise the variables using the ordinary normal distribution in order to calculate these probabilities.

“Z = (X - μ) / σ

For X = 1.50 mm:

Z = (1.50 - 1.50) / 0.01 = 0

For X = 1.56 mm

Z = (1.56 - 1.50) / 0.01 = 6”

One can determine the probability using a conventional normal distribution table or calculator.

Therefore,

“P (1.50 < X ≤ 1.56) = P(X ≤ 1.56) - P(X ≤ 1.50)

= P (Z ≤ 6) - P (Z ≤ 0)

= 1 - 0.5

= 0.5”

Hence the probability that an acceptable screw has a diameter which is greater than 1.50 mm is 0.5 or 50% (Dipto et al. 2020).

Question 5.

The median value of the given dataset which is given in the question is 93.5.

The mode value of the given dataset which is given in the question is 97.

The mode value of the given dataset which is given in the question is 72.

The sample size value of the given dataset which is given in the question is 30.

The sample mean value of the given dataset which is given in the question is approximately 85.5333.

The sample standard deviation value of the given dataset which is given in the question is approximately 16.122 (Bruce et al. 2020).

Question 6.

a)

1. The formula for the confidence interval must be used to get the Lower Limit (LL):

“LL = X? - z (σ/√n)

Where:

X? = the sample mean = 110

σ = the population standard deviation = 16

n = the sample size = 12

Z (α/2) = the z-score corresponding to the level of confidence, which for a 95% confidence interval is 1.96”

The z-score for a two-tailed test is 1.96, assuming a 95% degree of confidence.

Using the values in the formula as replacements:

“LL = 110 - 1.96 * 16 / √12

LL = 110 - 7.03

LL = 102.97.”

Hence, assuming a known population standard deviation, the mean IQ for students enrolled in this course has a 95% confidence interval of “(102.97, ∞).”

1. One can utilize the following formula to calculate the upper limit (UL) of the 95% confidence interval for the mean IQ of students taking this course:

“UL = x? + z* (σ / √n)”

Where n is the sample size (12), x is the sample mean (110), is the population standard deviation (16), and z* is the z-score that corresponds to a 95% confidence level. The z-score with a 95% confidence level, as determined by the z-table, is 1.96 when these values are inserted into the formula,

“UL = 110 + 1.96 * (16 / √12)

= 110 + 7.03

= 117.03”

Thus, the 95% confidence interval's upper limit (UL) for the mean IQ of students enrolled in this course is 117.03.

b)

1. One is able to utilize the following formula to calculate the Lower limit (LL) of the 95% confidence interval:

LL = x? - (tα/2 * (s/√n))

“Where:

x? = sample mean = 110

tα/2 = t-value for the 95% confidence interval with 11 degrees of freedom (df = n - 1) = 2.201

s = sample standard deviation = 14.5

n = sample size = 12”

“LL = 110 - (2.201 * (14.5/√12))

LL = 110 - 11.93

LL = 98.07”

Thus, 98.07 is the Lower limit (LL) of the 95% confidence interval for the mean IQ of the participants in this study.

1. The formula below can be used to get the upper limit (UL) for the 95% confidence interval.

UL = X? + (tα/2 * (s/√n))

Where s is the sample standard deviation, n is the sample size, X is the sample mean, and t/2 is the significant level of the t-distribution with (n-1) degrees of freedom at the alpha level of significance.

The sample size is n = 12, the sample mean is X = 110, and the sample standard deviation is s = 14.5; these numbers are provided to us.

One must establish the degrees of freedom (df) for the t-distribution in order to calculate the value of t/2. Since n = 12, df = n - 1 = 11 due to the number of degrees of freedom. The critical value of t for a 95% confidence interval with 11 degrees of freedom is roughly 2.201, according to a t-table or calculator.

“UL = 110 + (2.201 * (14.5/√12))

UL ≈ 128.37”

Hence, the mean IQ for students enrolled in this course has an upper limit of about 128.37 within the 95% confidence interval (Qi et al. 2020).

Question 7

One can utilise the “sample mean, sample size, the population mean, and population standard deviation” to do a one-sample t-test to see if the average price per square foot for warehouses has changed. The “alternative hypothesis is that it has changed, and the test's null hypothesis is that the population mean price per square foot for warehouses is still $32.28”.

To get the t-statistic, one can use the formula below.

“t = (x? - μ) / (s / sqrt (n))”

“Where n is the sample size, x? is the sample mean, μ is the population mean, s is the population standard deviation,”

“t = (32.67 - 32.28) / (1.29 / sqrt (49))

t = 2.33.”

The crucial value for a 5% level of significance is determined by a one-tailed t-distribution table with 48 degrees of freedom (df = n - 1). This value is 1.677.

One could reject the null hypothesis and conclude that the average price per square foot for warehouses has grown at a 5% level of significance because our calculated t-statistic (2.33) is higher than the crucial value (1.677).

As an alternative, one can draw a statistical inference using the p-value method. The p-value represents the likelihood that, if the null hypothesis were true, the sample mean would be as severe as ours or even more extreme.

The p-value for a one-tailed test with a t-statistic of 2.33 is roughly 0.012 using a t-distribution table with 48 degrees of freedom. Here it can be rejected the null hypothesis and conclude that the average price per square foot for warehouses has grown at a 5% level of significance because the p-value (0.012) is less than the 5% threshold of significance.

Part B: Python

Question 8

a) “Suppose A= {2, 5, 6} and B= {2, 6, 5}. Then A==B is a true statement true in Python. In Python, the order of elements in a set does not matter, so A and B are equivalent sets and A==B would return True.” Sets in Python are unsorted collections of distinct elements. The order of the elements in a set is not maintained as they are kept in a hash table. The == operator would compare two sets that contain the same elements, even if they are arranged differently, as equal.

b) Print () is a built-in function in Python and is a true statement. Python's built-in print () method is used to show output on the screen.

Question 9

The option ‘a’ “[1, 2, 3]” is an example of the list in the python language syntax.

Question 10

“The correct definition for the function to calculate y=-x^ (-t) is:

1. c) def cube(x,t):

return -x ** (-t)

This function takes two arguments, x and t, and returns the negative of x to the power of negative t, which is equivalent to -1/(x^t).”

Question 11.

“The variable A should be assigned to the number of elements in the first dimension of the array arr, which is the number of rows. Therefore, the correct answer is an option:

1. b) arr. Shape[0]

arr. shape[0] returns the first element of the shape tuple, which represents the number of rows in the array arr. Therefore, this is the correct option.”

Question 12.

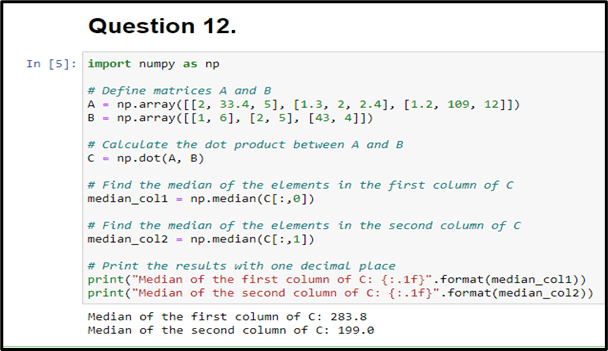
Figure 1: Python coding for Question 12

Using the NumPy library, this code creates the matrices A and B, calculates their dot product, and stores the outcome in matrix C. The median of the elements in C's first and second columns is then calculated, and the results are saved in the variables median col1 and median col2, respectively (El Hachimi et al. 2022).

Question 13.

The statement ‘a’ Functions are reusable pieces of programs is a correct statement here. Functions are modular, effective, and simpler to maintain bits of code that can be called from several places in a programme.

Question 14.

“The incorrect statement is (d):

A={"student ", "course ", "module ", "module code"}

A.add("marks")

“The reason why it is incorrect is that the syntax used for creating the set A is incorrect. Using curly braces ({}) to create a set creates an empty set, and the elements of a set should be separated by commas. Additionally, sets do not have an append method, but they have an additional method to add a new element to the set.” Therefore, to fix this statement, one can use the correct syntax to create the set A and then use the add method to add the new element "marks", like this:

A={"student ", "course ", "module ", "module code"}

A.add("marks")”

Question 15.

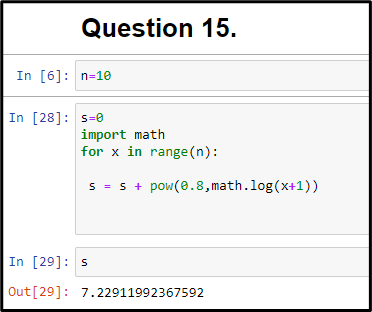
Figure 2: The code verification in Python

“Option (a) is the correct Python snippet to calculate Explanation: The expression to be calculated is ∑_(i=1)^n?0.8?^ln?i. One can rewrite the exponent using the property that ln(a^b) = b ln(a).

So,

ln?(i) = ln?(e^ln?(i)) = ln?(e^(ln?(i)*ln?(e))) = ln?(e^(ln?(i)*ln?(2.718))) = ln?(2.718^(ln?(i)))

Therefore,

0.8^ln?(i) = (2.718^ln?(0.8))^ln?(i) = 2.718^(ln?(0.8)*ln?(i))

Now, one can use this expression in the Python code. Option (a) correctly uses the expression above with the math library to calculate the sum.”

Question 16.

“Statement (a) would produce an error message because of np. sum () function expects an array as an argument, but in this statement, it is being passed a list containing two arrays (arr1 and arr2) as elements.”

Question 17.

“Option C is correct for the problem in the question.

Option A has syntax errors in the second and fourth conditions (missing "x =="), which would cause the code to fail (Lazzeri, 2020).

Option B has a syntax error in the second condition (missing "x =="), which would cause the code to fail.

Option C correctly checks for the lower and upper limits of each income band using the inclusive range operator (<=) and assigns the appropriate tax rate.

Option D is identical to Option B, which has a syntax error in the second condition (missing "x =="), and would cause the code to fail.”

Question 18.

All rows from both tables are returned in a “Full join which is option d”. It returns NULL if there isn't a match in any of the tables. Thus, you should utilise the complete join method to create a table with the most possible rows. This is so that it returns every row from both tables, whether or not there is a match.

References

Berti, A., Van Zelst, S.J. and van der Aalst, W., 2019. Process mining for python (PM4Py): bridging the gap between process-and data science. arXiv preprint arXiv:1905.06169.

Bruce, P., Bruce, A. and Gedeck, P., 2020. Practical statistics for data scientists: 50+ essential concepts using R and Python. O'Reilly Media.

Dipto, I.C., Rahman, M.A., Islam, T. and Rahman, H.M., 2020. Prediction of accident severity using artificial neural network: A comparison of analytical capabilities between python and R. Journal of Data Analysis and Information Processing, 8(3), pp.134-157.

Duli, S., 2021. THE ROLE OF PYTHON PROGRAMMING COURSE IN NATURAL SCIENCES. KNOWLEDGE-International Journal, 47(3), pp.469-472.

El Hachimi, C., Belaqziz, S., Khabba, S. and Chehbouni, A., 2022. Data Science Toolkit: An all-in-one python library to help researchers and practitioners in implementing data science-related algorithms with less effort. Software Impacts, 12, p.100240.

Holman, J.O. and Hacherl, A., 2022. Teaching Monte Carlo Simulation with Python. Journal of Statistics and Data Science Education, pp.1-12.

Jiang, D., 2021, June. Teaching Research of Business Data Analytics Course Based on Python. In 2021 6th International Symposium on Computer and Information Processing Technology (ISCIPT) (pp. 577-582). IEEE.

Lasser, J., Manik, D., Silbersdorff, A., Säfken, B. and Kneib, T., 2021. Introductory data science across disciplines, using Python, case studies, and industry consulting projects. Teaching Statistics, 43, pp.S190-S200.

Lazzeri, F., 2020. Machine learning for time series forecasting with Python. John Wiley & Sons.

Qi, Y., Peng, W. and Xiong, N.N., 2020. The effects of fiscal and tax incentives on regional innovation capability: text extraction based on python. Mathematics, 8(7), p.1193.

Sial, A.H., Rashdi, S.Y.S. and Khan, A.H., 2021. Comparative analysis of data visualization libraries Matplotlib and Seaborn in Python. International Journal, 10(1).

Suharjo, B., 2021. Application of K-Means Cluster and Spatial Statistics using Python to Analyze the Indicators of Indonesia Information Technology. Digital Zone: Jurnal Teknologi Informasi dan Komunikasi, 12(1), pp.11-18.

Xu, J. and Frydenberg, M., 2021. Python Programming in an IS Curriculum: Perceived Relevance and Outcomes. Information Systems Education Journal, 19(4), pp.37-54.