1. Introduction
1.1 Background
The Boston housing market, though characterised by complexity and multiple strands of factors dictating the going prices of real estate, has been studied for many decades. Housing prices in Boston have changed dramatically over time, following the dynamics of economic conditions and changing population demand for housing in the general housing sector. Its recent data reports that the median home price in Boston hit $600,000 over September in 2023, up 6.2% year-over-year (Woods, 2024). Boston real estate, being an educational and healthcare hub, as well as a technological hub, makes it one of the most sought-after cities to stay in the United States.
Other factors that shape Boston real estate pricing dynamics include property attributes, such as house size, number of bedrooms, and the age of the home (Xu, Zhang and Crabbe, 2024). Studies demonstrate properties located close to public transportation and educational institutions have typically higher values, with price premiums of up to 20% in some regions, as stated by Zhou et al. (2022). This study models these factors with machine learning techniques for the prediction of house prices while providing actionable insights for both would-be homeowners and real estate investors.
1.2 Research Aim, Objectives, and Questions
1.2.1 Research Aim
The aim of this study is to evaluate the influence of factors like property attributes on house prices in Boston.
1.2.2 Research Objectives
- To examine the impact of property attributes such as the number of bedrooms, property area and lost size on house prices in Boston
- To evaluate the influence of whether a house was built in colonial style or not on overall house price in Boston
- To develop Multiple Linear Regression Model in Excel in order to evaluate the impact of property attributes, property style and assessed property value on Boston house price.
1.2.3 Research Questions
- What are the impacts of property attributes such as the number of bedrooms and lot size on house prices in Boston?
- What is the influence of whether a house was built in colonial style or not on overall house price in Boston?
- What is the overall performance of the Multiple Linear Regression model in house price prediction?
1.3 Research Significance
This study helps in rendering valuable information on the factors that influence house prices in Boston, mainly because housing remains a significant investment for many individuals and families. Understanding what influences property values provides valuable information to buyers, sellers, and investors. The study is done concerning the relationship between property attributes, like the size of the house and bedrooms, and factors like location within the city. Therefore, through the identification of these main determinants, the research can provide predictive insights into the dynamics of the housing market, building on the anticipation of price trends. At the same time, the findings also guide policymakers in addressing issues of housing affordability and urban development. Real estate professionals could leverage the models developed in the study to improve their pricing strategies and hence optimise their investments. In general, this entire research mainly helps create an even more transparent and informed real estate market.
1.4 Research Methodology Overview
This research helps to predict house prices in Boston City, given the influence of property attributes on real-estate market. The primary objective is to develop a predictive regression model that can be used to generate accurate price predictions related to factors like lot size, bedrooms, and proximity to central areas. These research objectives involve explaining the relationship between these attributes and housing prices, evaluating the impact of property attributes, as well as developing predictive models to enhance the accuracy of house price predictions.
To achieve these objectives, data from the Boston housing dataset are going to be analysed using various statistical and machine learning techniques such as multiple linear regression, correlation analysis, and t-tests. The data visualisations also complement the analysis to better understand the interpretation of results. This research uses both logged and unlogged variables to look at their impact on price predictions. Thus, this study, in providing light on factors driving housing prices, helps to inform choices in real estate, and investment strategies, and be held to make decisions in policy reforms.
2. Literature Review
2.1 Impact of Property Attributes on House Prices
It has been a very common aspect of research to consider the impact of property attributes on house prices, with some key features frequently and influential. In particular, property size, the number of bedrooms, and the total square footage became a very significant factor when determining the value of a home (Karbalaee, 2023). Research by Zulkifley et al. (2020) found that these factors are among the strongest predictors of house prices. Furthermore, lot size has been determined to have a positive relationship with the value of the property because more land usually offers better privacy and scope for growth (Clapp, Cohen, and Lindenthal, 2021). In addition, the age and the state of a property are crucial because newer homes or well-kept properties usually fetch higher prices. Studies have further pointed to the role of aesthetic features like architectural style. For example, according to Nia and Rahbarianyazd (2020), homes in desired styles like Colonial have fetched higher premiums. Overall, these previous research studies mainly underscore the multifaceted nature of property attributes in shaping real estate prices.
Studies find that properties closer to the urban hubs or major routes usually come at a premium as they save time and provide easy access (Qin et al., 2023). The attributes of property areas in terms of social atmosphere like places with good schools, parks, and other public services tend to have a positive effect on the rise of property prices (Boys and Jeffery, 2023). Additionally, the study by Liu et al. (2022) stated that houses within high-performing school districts and distance from nearby marketplace command very high values compared to properties that located far away from market places and schools. Therefore, based on findings of past studies, it can be outlined that factors like property attributes (such as property area, number of bedrooms, assessed market price, property condition) can have a substantial influence on all price of houses.
2.2 Effectiveness of Log-Transformed Variables in House Price Prediction
In house price prediction, log-transformed variables can have substantial influence on the improvement of performance of a model when dealing with skewed data. House price data are typically right-skewed, leading to biassed estimates if not transformed properly (Algahtani, 2022). Normalising log skewness helps in regression analysis by making the data more appropriate (Hammouri et al., 2020). For example, it has been discovered that log transformation of the dependent variable (price) helps to obtain more stable and robust models, as extreme outliers are reduced in their impact (Mora-Garcia, Cespedes-Lopez, and Perez-Sanchez, 2022). Furthermore, coefficient values in log-transformed variables can be interpreted more meaningfully since they inform readers about percentage changes rather than absolute ones. Studies by Li (2023), also point out that log transformations enhance the accuracy of prediction models, especially where such markets have huge variability in prices, as is observed in real estate markets. This method, therefore improves predictive model performance by overcoming any non-linear relationship exhibited in the house price data. Thereby, it can be stated that logarithmic transformation of features can be a reliable solution for treating skewness in features within a linear regression model. However, the challenges associated with logarithmic transformation is the low interpretability of the features as they are not in the original scale of the features.
2.3 Implication of business analytics in the prediction of house prices
House price prediction is one of the major applications that business analytics provides to both house-buying and selling professionals. It uses data-driven techniques that involve machine learning and regression analysis to identify patterns and correlations between the attributes of properties, and market trends (Mathotaarachchi, Hasan, and Mahmood, 2024). For example, research work has shown that the adoption of high analytics improves the quality of the pricing models used so that predictions are more correct and timelier for house pricing (Rey-Blanco, Zofío and González-Arias, 2024). The updated pricing strategy is according to emerging conditions in the marketplace because they can be adjusted in real-time. Also, predictive models in real estate improve investment strategies by predicting future trends so that investors can make informed judgments (Veluru, 2023). Business analytics application also helps in managing risk through the detection of market fluctuations, hence being a key aspect of enhancing efficiency and profitability in the housing market.
2.4 Theoretical Underpinning
The entire research study is to predict the Boston house price based on the crucial key factors and property attributes underpinning the “Hedonic Pricing Theory”. Hedonic Pricing Theory explains how the price of a good or service involving a house, is contingent upon its characteristics (Rosen, 1974). This theory argues that house prices vary with some property attributes, such as size and number of bedrooms and location, but also depend on external factors, such as proximity to amenities and safety [Refer to Figure 1]. This theory is related to real estate, and states how much buyers pay more due to desirable features like larger lot sizes or better locations, so it is suited perfectly to analyse the impact of such attributes on housing prices.
Figure 1: Hedonic Pricing Theory
3. Data Description
3.1 Data Collection and Directory
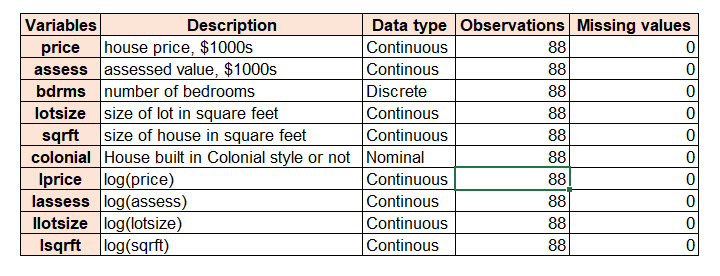
Table 1: Data description
The study mainly uses real estate pages from the Boston Globe in 1990, detailing homes that sold in the Boston, Massachusetts area of the USA. Data 1 in Table 1 consists of 88 records with no missing values and involves 10 significant variables describing property attributes and house prices. Among them are continuous variables like price (house price in $1000s), assess (assessed value in $1000s), lotsize (size of the lot in square feet), and ‘sqrft’ (size of the house in square feet). Apart from these variables the dataset also involves ‘bdrms’ (number of bedrooms) while colonial indicates whether the house is built in colonial style. Moreover, log-transformed variables such as “lprice”, “lassess”, “llotsize”, and “lsqrft” offer normalised values to analyse.
3.2 Variables Description
The selected Data1 data set mainly contains some variables that drive the entire analysis of house prices in the Boston area. Price and ‘assess’ are critical variables representing the house price and assessed value, respectively, in $1000s, both variables useful for capturing market valuation. Bdrms represents the number of bedrooms as a discrete variable affecting the price, whereas lotsize and sqrt correspond to the size of the lot and the house in terms of square feet with more considerable houses typically fetching higher prices. Colonial indicates if the house is colonial style and this might positively influence the house value based on aesthetic preferences. Other log-transformed variables involve “lprice”, “lassess”, “llotsize”, and “lsqrft” which help to transform skew data on the variables to better improve model output accuracy and interpretability. Understanding the variables aids in the determination of the causes of housing prices in the Boston market.
4. Empirical Analysis
4.1 Selection of Methods
This study uses statistical and analytical approaches to assess factors that influence house prices. Summary statistics describe the dataset, which gives information on central tendencies and the actual distribution of the data. Data visualisations give illustrations of relationships and trends in variables, which supports intuitive insights. This t-test determines whether colonial-style homes significantly affect house prices, with prices as continuous and colonial as categorical. It further applies correlation analysis to identify the relationship among variables while avoiding multicollinearity. The third is multiple linear regression which helps to establish the predictiveness of characteristics like assessed value, bedrooms, lot size, and colonial style to house prices, thereby having robust conclusions.
4.2 Assumptions of the Chosen Methods
The t-test assumes a normal distribution of price data and equal variance of groups (colonial vs. non-colonial). Correlation analysis mainly assumes linearity among the relationships of variables whereas multiple linear regression assumes linearity, homoscedasticity, independence of residuals, and absence of multicollinearity, confirming accurate estimation of predictions such as assessed value, bedrooms, lot size, and colonial style on house prices.
5. Results/Discussion
5.1 Summary Statistics
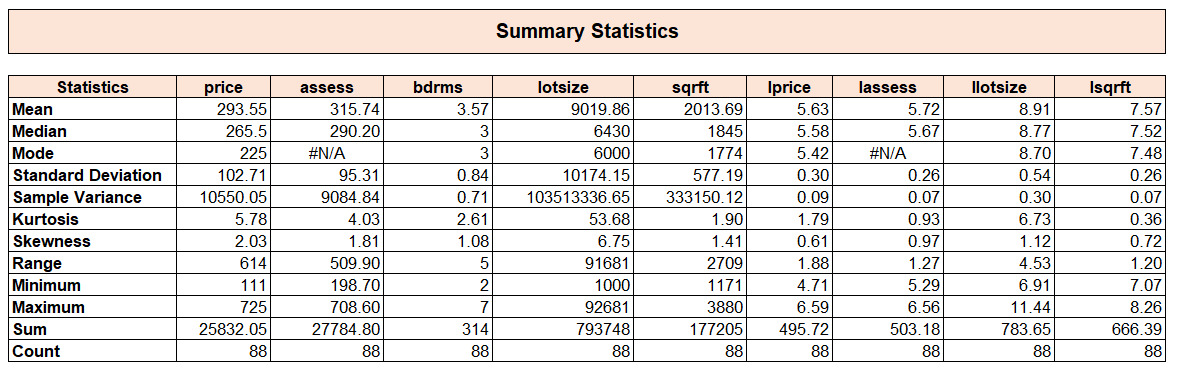
Table 2: Summary statistics
The dataset provides an interest in house prices and associated variables as shown in Table 2. Averagely, a house costs 293.55k, with a median of 265.5k, suggesting a slightly right-skewed distribution (skewness: 2.03). Assessed values average 315.74K, close to price whereas houses usually have 3-4 bedrooms (mean: 3.57). Lot sizes tend to be pretty variable (mean: 9,019.86 sq. ft.; std. dev.: 10,174.15) and skewed by larger houses. The average square footage is 2,013.69 sq. ft., reflecting standard mid-sized homes. Additionally, Log-transformed variables (e.g., lprice) ensure normality for regression. These statistics highlight data variability and relationships, justifying the methods used for analysis.
5.2 Data Visualisations
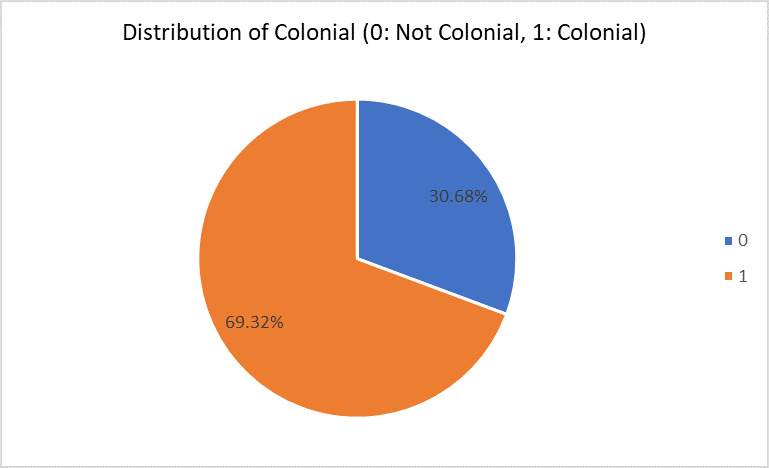
Figure 2: Colonial distribution
Figure 2 reveals that 69.32% of the homes are colonial, and 30.68% are non-colonial, which indicates a high dominance and may probably reflect the architectural history of Boston and a preference for more traditional designs, adding aesthetic and cultural appeal.
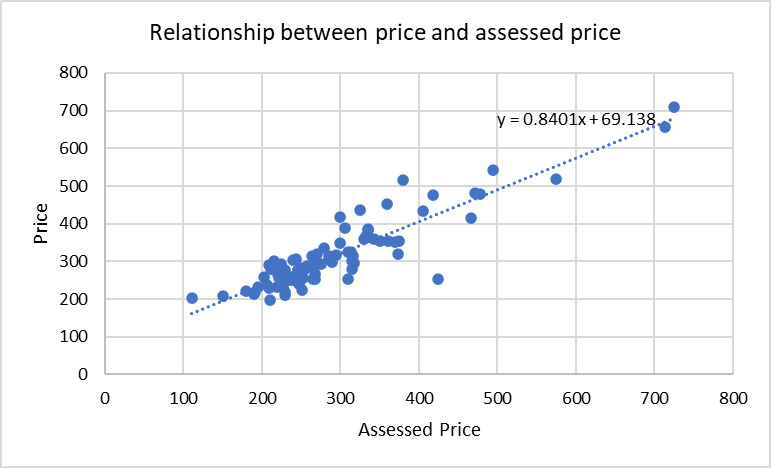
Figure 3: Relationship between price and assessed price
Figure 3 portrays the relationship, which indicates a positive correlation, showing that high-assessed prices correspond to higher house prices. This represents actual practice valuation because the assessed prices reflect market trends and the value of a property accurately.
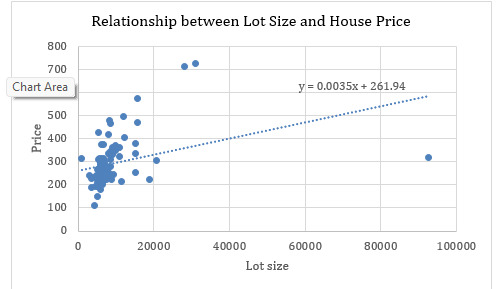
Figure 4: Lotsize Distribution
Price (y) = 0.0035 * lotsize + 261.94
The lot-size distribution is very skewed, with most of the observations falling below 20,000 square feet [refer to Figure 4]. Additionally, the factor lot size shows a low level of linear relationship, highlight lack of influence of lot size on overall price of houses in Boston.
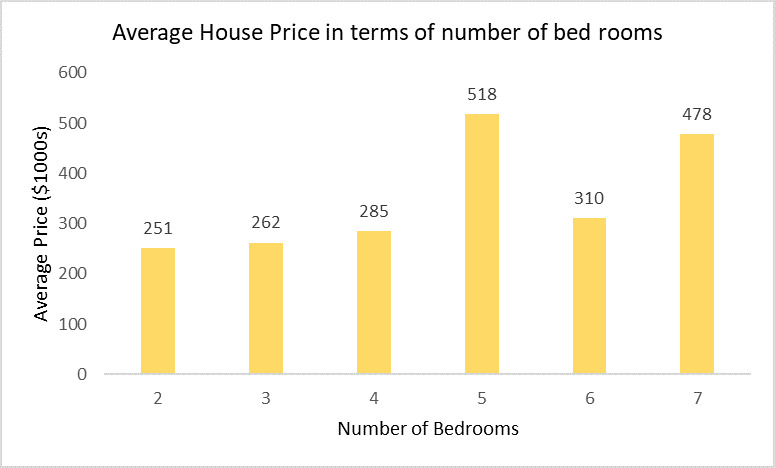
Figure 5: House price with number of bedrooms
Figure 5 compares the price of a house to the number of bedrooms and houses that have more rooms (5 and 7) are more costly. This indicates the high demand for such houses as most require living rooms with utmost functionality and much family accommodation.
5.3 t-Test: Two-Sample Assuming Equal Variances
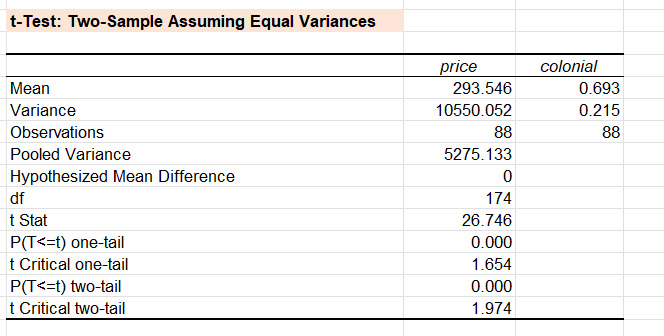
Table 3: Results obtained from t-test
- H0: House prices in Boston have shown no variation in whether the house was built in a colonial style.
- Ha: House prices in Boston have shown a significant variation in terms of whether the house was built in colonial style or not.
Table 3 shows the results obtained from the t-test (assuming equal variances). As per the viewpoint of Kim and Park (2019) and Rasch, Kubinger, and Moder (2011), the t-test is applicable for evaluating the distribution of normally distributed continuous variables over a categorical variable with two distinct categories. In this study, the variable ‘Price’ is continuous, while the variable ‘colonial’ is a categorical variable with two distinct categories (0 and 1), justifying the selection of the t-test for evaluating the association between price and colonial properties. The observed t-statistics is 26.746 with a p-value of 0.000, signifying rejection of the null hypothesis at a level of significance of 5% (Refer to Table 3). This leads to the inference that house prices in Boston have shown a significant variation in terms of whether the house was built in colonial style or not. The positive t-value (26.746) indicates that houses built in colonial architecture have higher prices compared to houses built in non-colonial style. The aesthetic or historical appeal of colonial architecture might have added significant value to the rise of house prices in Boston during 1990.
5.4 Correlation Analysis
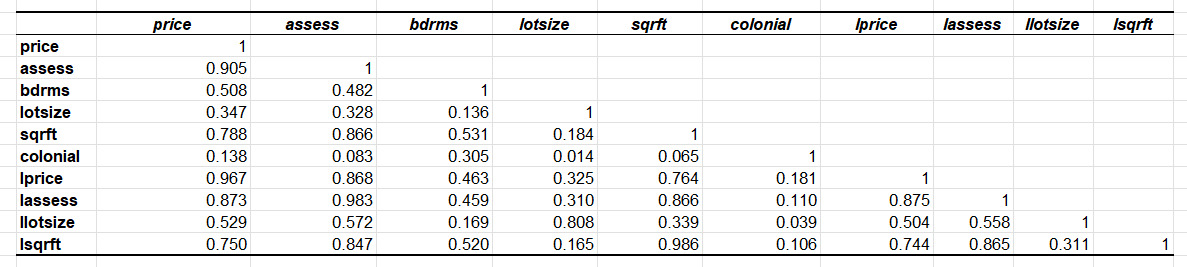
Table 4: Correlation analysis
From Table 4, it can be observed that the high positive correlation between Price and Assessed price (r = 0.905) indicates that house prices are strongly associated with their assessed values. This suggests that assessment can be a reliable indicator in the estimation of the market price of houses. Additionally, the strong positive correlation between Price and Square Footage (r = 0.788) implies that larger houses tend to have higher prices, as square footage is a key determinant of value. Factors like the number of bedrooms (r = 0.508) and lot size (r = 0.347) exhibit a moderate positive association with house prices, indicating that with the increase of availability of a higher number of bedrooms and larger lot size, the market prices of houses can show moderate hike.
The variables ‘lprice’, ‘lassess’, ‘llotsize’, and ‘lsqrft’ cause multicollinearity as the observed correlations between these features are outside the range of ±0.70 (Refer to Table 4). These variables are flagged as showing multicollinearity as these features (independent variables) are exhibiting a strong association between them, which can introduce biases in regression analysis. As per the viewpoint of Chan et al. (2022), multicollinearity refers to strong correlations between the features (with Pearson’s Correlation Coefficient of greater than +0.70 and less than -0.70), which can lead to biases in statistical analysis. Due to this, these variables have not been included in Multiple Linear Regression analysis, which has enhanced the overall explanation power of the multiple linear regression model.
5.5 Multiple Linear Regression
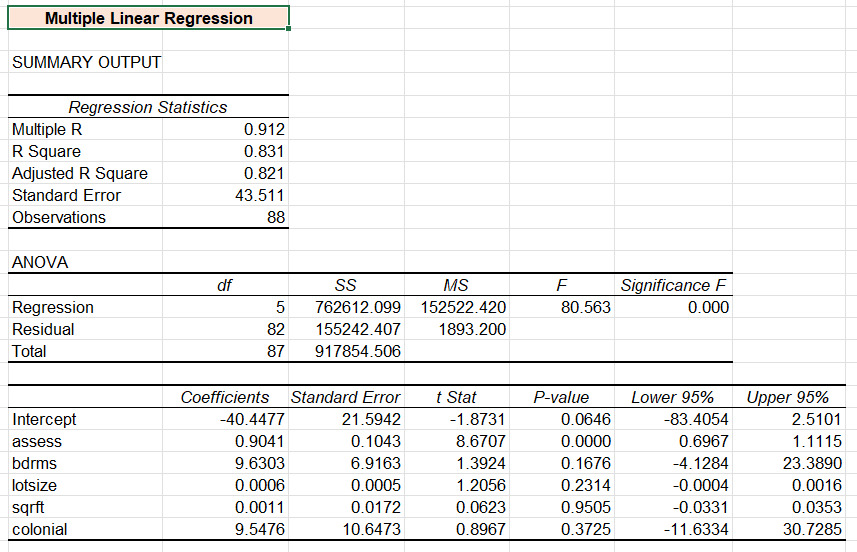
Table 5: Multiple Linear Regression Model
The generalised observed equation of the multiple linear regression equation can be represented as:
Price (y) = a + b1 * assess + b2 * bdrms + b3 * lotsize + b4 * sqrft + b5 * colonial ……… (Equation 1).
The equation obtained from the Multiple Linear Regression model can be represented as:
Price (y) = -40.447 + 0.9041 * assess + 9.6303 * bdrms + 0.0006 * lotsize + 0.0011 * sqrft + 9.5476 * colonial ……… (Equation 2).
The main motive of conducting the Multiple Linear Regression analysis is to evaluate the influence of property attributes (such as lot size, number of bedrooms, property area, and property style (colonial)) on the variation of property prices. The obtained R-square value of the Multiple Linear Regression model is 0.831, indicating the model explains approximately 83.1% variability in the target variable (price), which is considerably high. The Multiple R value of 0.912 indicates a high level of the linear relationship between features (lot size, number of bedrooms, property area, and property style (colonial)) on house prices (Refer to Table 5 and Appendix 1).
Moreover, the F-statistics of the model is 80.563 with a p-value of 0.000 (<0.05), indicating statistical significance of the model at a level of significance of 1%. This shows that the results obtained from the multiple linear regression model are statistically significant.
The factors ‘assess’ exhibit a statistically significant positive influence on house price (with Coefficient = 0.9041, t-value = 8.670, and p-value = 0.000) at a level of significance of 1%. This indicates that assessed value is a strong positive predictor of house price: a unit increase in assessed value corresponds to a 0.9041 increase in price, holding other factors constant. On the other hand, other attributes such as the number of bedrooms (bdrms) (Coefficient = 9.6303, t-value = 1.392, p-value = 0.1676), lotsize (Coefficient = 0.0006, t-value = 1.2056, p-value = 0.2314) and ‘sqrft’ (Coefficient = 0.0011, t-value = 0.0623, p-value = 0.9505) exhibit no statistically significant influence variations in house prices. This leads to the inference that the assessed market price of houses create a statistically significant positive impact on overall property prices in Boston. The obtained line fit plots for all the features have been presented in Appendix 1.
5.6 Discussions
This section discusses the entire analysis of this study concerning the previously mentioned research studies related to this context. Literature indicates that key determinants of house prices are property attributes, which include the number of bedrooms, lot size, and architectural style, among others (Karbalaee, 2023; Clapp, Cohen, and Lindenthal, 2021). Further, Nia and Rahbarianyazd (2020) studies reflected a higher premium for buildings with colonial architecture. Additionally, factors such as proximity to urban centres and safety significantly correlate with price (Qin et al., 2023; Ceccato and Wilhelmsson, 2019). Therefore, it can be shown that real estate valuation is multi-faceted, potentially having influence of property attributes and market condition on overall rise of property prices.
From the analysis, house price variation positively correlates with assessed value and square footage, consistent with extant literature. The predictive reliability of a high assessed price is further supported by prior findings as shown in correlation (r = 0.905). Unlike previous studies by Mora-Garcia et al. (2022), the statistical significance of the number of bedrooms was low and indicates localised market preferences. Colonial architecture is seen to uniquely contribute to aesthetic value being the prime driver through validation through the t-test. In addition to that, this entire analysis is different because it incorporates advanced statistical methods like log transformation and multiple linear regression to reduce skewness in data and increase the precision of the model. Thus, the focus on colonial architecture in Boston makes the analysis culturally important to understand the dynamics of housing prices.
5.7 Limitations
- The data is collected from real estate pages of the Boston Globe during 1990, indicating outdated data. The evaluation of outdated data for house price can limits it relevance in contemporary time.
- The considerably low number of samples (88) can limit this study in terms of generalisability.
- The non-consideration of geographic location related factors like distance from nearby market places or whether the property is in urban or semi-urban areas can limit this study in terms of generalisability and depth of findings.
5.8 Future Scope
- Future study can consider geographic locations (such as distance from nearby market places or whether the property is in urban or semi-urban areas) as the determinants of house price.
- Additionally, future study can focus on collection of contemporary data related to property attributes and house prices. This can possibly enhance the reliability and applicability of the findings in real-world scenario of house price prediction.
6. Conclusion
This entire study assessed different significant factors that influence Boston house prices by using the attributes of properties, location, and modelling. The key findings are that the size of the property, number of bedrooms, and lot size are significant factors that affect house prices, and Colonial-style homes have attracted higher premiums. In addition to that, location near amenities and public transport occurred as a critical determinant, often commanding a substantial price premium. Moreover, log-transformed variables improved the performance of the models by eliminating skewness in data, providing more robust predictions. Furthermore, Multiple Linear Regression captured the dynamics quite well, offering useful information to buyers, sellers, investors, and policymakers. In a nutshell, these findings support “Hedonic Pricing Theory” as they demonstrate significant property features along with the specific locations that adequately affect the prices of real estate.
If you need expert guidance in completing analytical projects like this, Native Assignment Help provides professional Assignment Help for students across the UK. Their academic specialists assist with data analysis, regression modelling, and case study writing, ensuring high-quality, plagiarism-free submissions tailored to university standards.
References
Algahtani, S.N. (2022). Constructing a House Price Index for Saudi Arabia. Journal of Real Estate Portfolio Management, pp.1–17. doi: https://doi.org/10.1080/10835547.2022.2105530.
Boys, J. and Jeffery, A. (2023). Valuing Urban Schools as Social Infrastructure. pp.113–130. doi: https://doi.org/10.1007/978-981-19-9972-7_8.
Ceccato, V. and Wilhelmsson, M. (2019). Do crime hot spots affect housing prices? Nordic Journal of Criminology, [online] 21(1), pp.1–19. doi: https://doi.org/10.1080/2578983x.2019.1662595.
Chan, J.Y.-L., Leow, S.M.H., Bea, K.T., Cheng, W.K., Phoong, S.W., Hong, Z.-W. and Chen, Y.-L. (2022). Mitigating the Multicollinearity Problem and Its Machine Learning Approach: A Review. Mathematics, [online] 10(8), p.1283. doi: https://doi.org/10.3390/math10081283.
Clapp, J.M., Cohen, J.P. and Lindenthal, T. (2021). Are Estimates of Rapid Growth in Urban Land Values an Artifact of the Land Residual Model? The Journal of Real Estate Finance and Economics. doi: https://doi.org/10.1007/s11146-021-09834-4.
Hammouri, H.M., Sabo, R.T., Alsaadawi, R. and Kheirallah, K.A. (2020). Handling Skewed Data: A Comparison of Two Popular Methods. Applied Sciences, 10(18), p.6247. doi: https://doi.org/10.3390/app10186247.
Karbalaee, M. (2023). Analysis on the House Prices Dataset. [online] doi: https://doi.org/10.13140/RG.2.2.18256.72960.
Kim, T.K. and Park, J.H. (2019). More about the basic assumptions of t-test: normality and sample size. Korean Journal of Anesthesiology, [online] 72(4), pp.331–335. doi: https://doi.org/10.4097/kja.d.18.00292.
Li, Y. (2023). Analysis of Real Estate Predictions Based on Different Models. Highlights in science, engineering and technology, 76, pp.410–414. doi: https://doi.org/10.54097/vbmqmh04.
Liu, Z., Ye, J., Ren, G. and Feng, S. (2022). The Effect of School Quality on House Prices: Evidence from Shanghai, China. Land, 11(11), p.1894. doi: https://doi.org/10.3390/land11111894.
Mathotaarachchi, K.V., Hasan, R. and Mahmood, S. (2024). Advanced Machine Learning Techniques for Predictive Modeling of Property Prices. Information, [online] 15(6), p.295. doi: https://doi.org/10.3390/info15060295.
Mora-Garcia, R.-T., Cespedes-Lopez, M.-F. and Perez-Sanchez, V.R. (2022). Housing Price Prediction Using Machine Learning Algorithms in COVID-19 Times. Land, [online] 11(11), p.2100. doi: https://doi.org/10.3390/land11112100.
Nia, H.A. and Rahbarianyazd, R. (2020). Aesthetics of Modern Architecture: A Semiological Survey on the Aesthetic Contribution of Modern Architecture. Civil Engineering and Architecture, 8(2), pp.66–76. doi: https://doi.org/10.13189/cea.2020.080204.
Qin, Y., Zhang, Y., Yao, M. and Chen, Q. (2023). How to Measure the Impact of Walking Accessibility of Suburban Rail Station Catchment Areas on the Commercial Premium Benefits of Joint Development. Sustainability, [online] 15(6), p.4897. doi: https://doi.org/10.3390/su15064897.
Rasch, D., Kubinger, K.D. and Moder, K. (2011). The two-sample t test: pre-testing its assumptions does not pay off. Statistical Papers, [online] 52(1), pp.219–231. doi: https://doi.org/10.1007/s00362-009-0224-x.
Rey-Blanco, D., Zofío, J.L. and González-Arias, J. (2024). Improving hedonic housing price models by integrating optimal accessibility indices into regression and random forest analyses. Expert Systems with Applications, 235, pp.121059–121059. doi: https://doi.org/10.1016/j.eswa.2023.121059.
Rosen, S. (1974). Hedonic Prices and Implicit Markets: Product Differentiation in Pure Competition. Journal of Political Economy, [online] 82(1), pp.34–55. Available at: https://www.jstor.org/stable/1830899.
Veluru, C.S. (2023). Revolutionizing Real Estate: AI-Driven Insights from Historical Data for Smart Property Decisions. Journal of Artificial Intelligence & Cloud Computing, [online] 2(1), pp.1–11. doi: https://doi.org/10.47363/jaicc/2023(2)376.
Woods, E. (2024). Greater Boston home prices tumble from summer highs. [online] Boston.com. Available at: https://www.boston.com/real-estate/home-buying/2024/10/23/greater-boston-home-prices-tumble-from-summer-highs/ [Accessed 22 Nov. 2024].
Xu, J., Zhang, Z. and Crabbe, J.C. (2024). Multiscale Impacts of Land Environmental Features and Planning on Apartment Resale Prices in Jinan City, China. Land, [online] 13(7), pp.954–954. doi: https://doi.org/10.3390/land13070954.
Zhou, Y., Tian, Y., Jim, C.Y., Liu, X., Luan, J. and Yan, M. (2022). Effects of Public Transport Accessibility and Property Attributes on Housing Prices in Polycentric Beijing. Sustainability, 14(22), p.14743. doi: https://doi.org/10.3390/su142214743.
Zulkifley, N.H., Rahman, S.A., Ubaidullah, N.H. and Ibrahim, I. (2020). House Price Prediction using a Machine Learning Model: A Survey of Literature. International Journal of Modern Education and Computer Science, 12(6), pp.46–54. doi: https://doi.org/10.5815/ijmecs.2020.06.04.
